Population structure inference using discriminant analysis

Xinghu Qin –School of Biology, University of St Andrews

30-03-2020

Source: vignettes/DA.Rmd

Instruction

This vignette demonstrates the implementation of supervised learning in ecological and evolutionary inference. In this vignette, we take the microsatellite genotypes of 15 cattle breeds (Laloë et al. 2007) as an example. We aim to use different supervised leaning techniques to identify the population structure of 15 cattle breeds.

Practical analyses

We use the microsatellite genotypes of 15 cattle breeds (Laloë et al. 2007) as an example to show population structure inference and visualization. We compare six approaches that are feasible and suitable for population structure inference here. We use the commonly used unsupervised learning technique, PCA, as the benchmark. We demonstrate how to use these five supervised learning approaches, including DAPC, LFDAPC, LFDA, LFDAKPC, and KLFDA, to identify population structure. These five supervised learning techniques are all from the same discriminant family.

First, we need to install and load the package.

Install DA

#Install from CRAN
#install.packages("DA")
## or you can get the latest version of HierDpart from github
library(devtools)

install_github("xinghuq/DA")

Preparing the data.


library("DA")
# example genepop file
f <- system.file('extdata',package='DA')
infile <- file.path(f, "Cattle_breeds_allele_frequency.csv")
Cattle_pop=file.path(f, "Cattle_pop.csv")
cattle_geno=read.csv(infile,h=T)
cattle_pop=read.csv(Cattle_pop,h=T)

Principal Component Analysis (PCA)

PCA is still one of the most commonly used approaches to study population structure. However, PCs represent the global structure of the data without consideration of variation within classes.

cattle_pop$x=factor(cattle_pop$x,levels = unique(cattle_pop$x))
### PCA
cattle_pc=princomp(cattle_geno[,-1])

#plot the data projection on the components
library(plotly)
# Loading required package: ggplot2
# 
# Attaching package: 'plotly'
# The following object is masked from 'package:ggplot2':
# 
#     last_plot
# The following object is masked from 'package:stats':
# 
#     filter
# The following object is masked from 'package:graphics':
# 
#     layout
   cols=rainbow(length(unique(cattle_pop$x)))
   p0 <- plot_ly(as.data.frame(cattle_pc$scores), x =cattle_pc$scores[,1], y =cattle_pc$scores[,2], color = cattle_pop$x,colors=cols[cattle_pop$x],symbol = cattle_pop$x,symbols = 1:15L) %>% 
     add_markers() %>%
     layout(scene = list(xaxis = list(title = 'PC1'),
                         yaxis = list(title = 'PC2')))

  
p0
# Warning: The shape palette can deal with a maximum of 6 discrete values
# because more than 6 becomes difficult to discriminate; you have
# 15. Consider specifying shapes manually if you must have them.

 

Fig.1 PCA plot of 15 cattle breeds.

Discriminant Analysis of Principal Components (DAPC)

Using DAPC to display the pop structure is a common means in population genetics. This can be achieved through “adegenet” package.

library(adegenet)
# Loading required package: ade4
# Registered S3 method overwritten by 'spdep':
#   method   from
#   plot.mst ape
# Registered S3 methods overwritten by 'vegan':
#   method      from
#   plot.rda    klaR
#   predict.rda klaR
#   print.rda   klaR
# 
#    /// adegenet 2.1.1 is loaded ////////////
# 
#    > overview: '?adegenet'
#    > tutorials/doc/questions: 'adegenetWeb()' 
#    > bug reports/feature requests: adegenetIssues()
cattle_pop$x=factor(cattle_pop$x,levels = unique(cattle_pop$x))
###DAPC
cattle_dapc=dapc(cattle_geno[,-1],grp=cattle_pop$x,n.pca=10, n.da=3)

#plot the data projection on the components
library(plotly)
   cols=rainbow(length(unique(cattle_pop$x)))
   p1 <- plot_ly(as.data.frame(cattle_dapc$ind.coord), x =cattle_dapc$ind.coord[,1], y =cattle_dapc$ind.coord[,2], color = cattle_pop$x,colors=cols[cattle_pop$x],symbol = cattle_pop$x,symbols = 1:15L) %>% 
     add_markers() %>%
     layout(scene = list(xaxis = list(title = 'LDA1'),
                         yaxis = list(title = 'LDA2')))

   p1
# Warning: The shape palette can deal with a maximum of 6 discrete values
# because more than 6 becomes difficult to discriminate; you have
# 15. Consider specifying shapes manually if you must have them.

 

Fig.2 DAPC plot of 15 cattle breeds. This is an interactive plot that allows you to point the data values and display the value as you wish.

Discriminant Analysis of Kernel Principal Components (DAKPC)

Discriminant analysis of kernel principal components (DAKPC) is a variant of DAPC. However, people try to incorporate the non-linear relationship between loci and samples, so that the kernel principal component analysis is emolyed to achieve this goal. Below is the implementation of DAKPC.

cattle_ldakpc=LDAKPC(cattle_geno[,-1],cattle_pop$x,n.pc=10)
# Loading required package: kernlab
# 
# Attaching package: 'kernlab'
# The following object is masked from 'package:ggplot2':
# 
#     alpha

 cols=rainbow(length(unique(cattle_pop$x)))
   p2 <- plot_ly(as.data.frame(cattle_ldakpc$LDs), x =cattle_ldakpc$LDs[,1], y =cattle_ldakpc$LDs[,2], color = cattle_pop$x,colors=cols[cattle_pop$x],symbol = cattle_pop$x,symbols = 1:15L) %>% 
     add_markers() %>%
     layout(scene = list(xaxis = list(title = 'LDA1'),
                         yaxis = list(title = 'LDA2')))
p2
# Warning: The shape palette can deal with a maximum of 6 discrete values
# because more than 6 becomes difficult to discriminate; you have
# 15. Consider specifying shapes manually if you must have them.

 

Fig.3 LDAKPC plot of 15 cattle breeds.

LDAKPC has the similar result with DAPC.

Local Fisher Discriminant Analysis (LFDA)

In comparison to LDA, LFDA not only considers the variation between classes, but also the variation within classes. Thus, LFDA can discriminate the multimodal data while LDA can not. LFDA is an upgraded version of LDA.

cattle_lfda=LFDA(cattle_geno[,-1],cattle_pop$x,r=3,tol=1E-3)
# Loading required package: lfda
# Loading required package: klaR
# Loading required package: MASS
# 
# Attaching package: 'MASS'
# The following object is masked from 'package:plotly':
# 
#     select

cols=rainbow(length(unique(cattle_pop$x)))
p3 <- plot_ly(as.data.frame(cattle_lfda$Z), x =cattle_lfda$Z[,1], y =cattle_lfda$Z[,2], color = cattle_pop$x,colors=cols[cattle_pop$x],symbol = cattle_pop$x,symbols = 1:15L) %>% 
     add_markers() %>%
     layout(scene = list(xaxis = list(title = 'LDA1'),
                         yaxis = list(title = 'LDA2')))
p3
# Warning: The shape palette can deal with a maximum of 6 discrete values
# because more than 6 becomes difficult to discriminate; you have
# 15. Consider specifying shapes manually if you must have them.

 

Fig.4 LFDA plot of 15 cattle breeds.

Local Fisher Discriminant Analysis of Kernel Principal Components (LFDAKPC)

As LFDA is more advanced than LDA, I adopt LFDA for discriminant analysis on the basis of LDAKPC. Now we get LFDAKPC, Local (Fisher) Discriminant Analysis of Kernel Principal Components (LFDAKPC). Below is the implementation of LFDAKPC.

cattle_lfdakpc=LFDAKPC(cattle_geno[,-1],cattle_pop$x,n.pc=10,tol=1E-3)

cols=rainbow(length(unique(cattle_pop$x)))
p4 <- plot_ly(as.data.frame(cattle_lfdakpc$LDs), x =cattle_lfdakpc$LDs[,1], y =cattle_lfdakpc$LDs[,2], color = cattle_pop$x,colors=cols[cattle_pop$x],symbol = cattle_pop$x,symbols = 1:15L) %>% 
     add_markers() %>%
     layout(scene = list(xaxis = list(title = 'LDA1'),
                         yaxis = list(title = 'LDA2')))
p4
# Warning: The shape palette can deal with a maximum of 6 discrete values
# because more than 6 becomes difficult to discriminate; you have
# 15. Consider specifying shapes manually if you must have them.

 

Fig.5 LFDAKPC plot of 15 cattle breeds.

The LFDAKPC also produces the similar results as LDAKPC and DAPC.

Kernel Local Fisher Discriminant Analysis (KLFDA)

Kernel local (Fisher) discriminant analysis (KLFDA) is a kernelized version of local Fisher discriminant analysis (LFDA). KLFAD can capature the non-linear relationships between samples. It was reported that the discrimintory power of KLFDA was significantly improved compared to LDA.

cattle_klfda=klfda_1(as.matrix(cattle_geno[,-1]),as.matrix(cattle_pop$x),r=3,tol=1E-10,prior = NULL)
# Loading required package: WMDB

cols=rainbow(length(unique(cattle_pop$x)))
p5 <- plot_ly(as.data.frame(cattle_klfda$Z), x =cattle_klfda$Z[,1], y =cattle_klfda$Z[,2], color = cattle_pop$x,colors=cols[cattle_pop$x],symbol = cattle_pop$x,symbols = 1:15L) %>% 
     add_markers() %>%
     layout(scene = list(xaxis = list(title = 'LDA1'),
                         yaxis = list(title = 'LDA2')))
p5
# Warning: The shape palette can deal with a maximum of 6 discrete values
# because more than 6 becomes difficult to discriminate; you have
# 15. Consider specifying shapes manually if you must have them.

 

Fig.6 KLFDA plot of 15 cattle breeds. KLFDA seems present the aggregates that are more convergent than the above methods.

All the above methods show the same global structure for 15 cattle breeds.

Individual assignment using Kernel Local Fisher Discriminant Analysis (KLFDA)

Kernel local (Fisher) discriminant analysis (KLFDA) is the optimal approach for population structurte inference when tested using this cattle data. Now, we plot the cattle individual membership representing the posterior possibilities of individuals as the population structure. This gives the similar plot produced from STRUCTURE software.



library(adegenet)
## asignment plot
compoplot(as.matrix(cattle_klfda$bayes_assigment$posterior),show.lab = TRUE, posi=list(x=5,y=-0.01),txt.leg = unique(cattle_pop$x))
&nbsp;

 

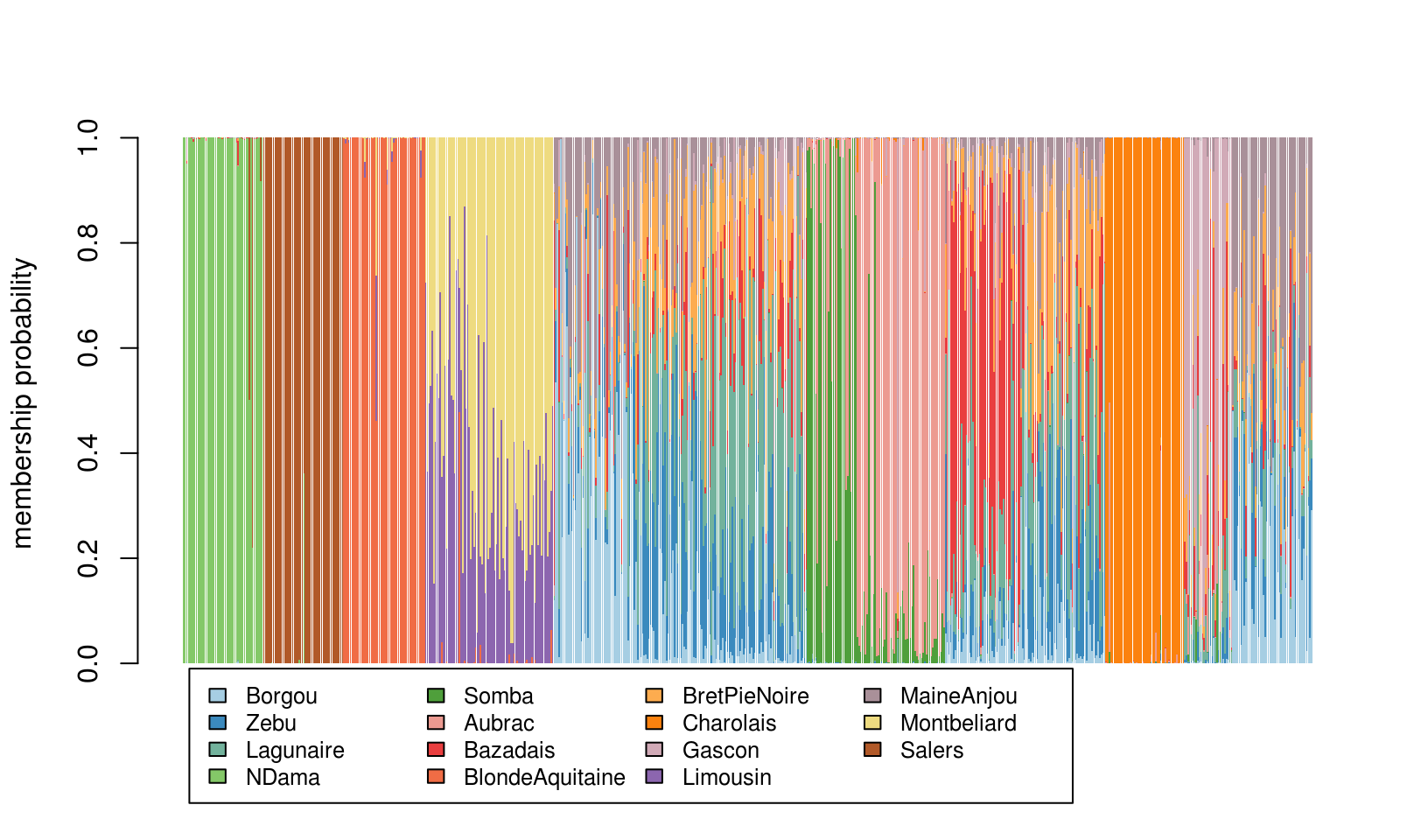
Fig. 7 The population structure of Cattle breeds (individual assignment)

References

Laloë, D., Jombart, T., Dufour, A.-B. & Moazami-Goudarzi, K. (2007). Consensus genetic structuring and typological value of markers using multiple co-inertia analysis. Genetics Selection Evolution, 39, 545.

Jombart, T. (2008). adegenet: a R package for the multivariate analysis of genetic markers. Bioinformatics, 24, 1403-1405. Sugiyama, M (2007).Dimensionality reduction of multimodal labeled data by local Fisher discriminant analysis. Journal of Machine Learning Research, vol.8, 1027-1061.

Sugiyama, M (2006). Local Fisher discriminant analysis for supervised dimensionality reduction. In W. W. Cohen and A. Moore (Eds.), Proceedings of 23rd International Conference on Machine Learning (ICML2006), 905-912.

Original Matlab Implementation: http://www.ms.k.u-tokyo.ac.jp/software.html#LFDA

Tang, Y., & Li, W. (2019). lfda: Local Fisher Discriminant Analysis inR. Journal of Open Source Software, 4(39), 1572.

Moore, A. W. (2004). Naive Bayes Classifiers. In School of Computer Science. Carnegie Mellon University.

Pierre Enel (2020). Kernel Fisher Discriminant Analysis (https://www.github.com/p-enel/MatlabKFDA), GitHub. Retrieved March 30, 2020.

Karatzoglou, A., Smola, A., Hornik, K., & Zeileis, A. (2004). kernlab-an S4 package for kernel methods in R. Journal of statistical software, 11(9), 1-20.

Bingpei Wu, 2012, WMDB 1.0: Discriminant Analysis Methods by Weight Mahalanobis Distance and bayes.

Ito, Y., Srinivasan, C., & Izumi, H. (2006, September). Discriminant analysis by a neural network with Mahalanobis distance. In International Conference on Artificial Neural Networks (pp. 350-360). Springer, Berlin, Heidelberg.

Wölfel, M., & Ekenel, H. K. (2005, September). Feature weighted Mahalanobis distance: improved robustness for Gaussian classifiers. In 2005 13th European signal processing conference (pp. 1-4). IEEE.